|
Electric power |
Work done
by electricity per unit time. |
| Joule
heat |
Heat generated
on a resistor when current I (ampere) flows
through a resistor with resistance R (ohm)
for time t (sec). Expressed by the following
equation.W=I©÷ R t / 4.186= 0.24 I©÷ R t (cal)
|
| Unit
of kilo calorie |
Amount of
heat energy necessary to raise the temperature
of 1 kg of water by 1oC. Expressed as 1 Kcal.
Can be expressed in Kcal or KWH.1 [Kcal] =
4186 (J) £ÛWatt.sec£Ý860 (Kcal) = 1 KWH |
| Ohm¡¯s
law |
If voltage
E (volt) is applied to a resistor with resistance
R (ohm), current I (ampere) flows, the relation
can be expressed as follows.I = E / R (A),
E = I R (V) and R = E / I (¥Ø)where, I = current
(ampere) (A), E = voltage (volt) (V) and R
= resistance (ohm) (¥Ø). |
| Composite
resistance of resistors connected in series |
If the resistors
are connected in series, current flowing through
each resistor is identical. Let the voltage
drop at each resistor V1, V2 and V3, respectively,
and the current I (A). Then V1 = I R1, V2
= I R2 and V3 = I R3.
...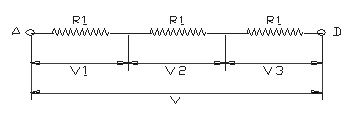
Since the voltage across AD is the same as
the sum of the voltage drop at each resistor,V
= V1+ V2+ V3= I R1 + I R2 + I R3= I (R1+ R2+
R3) |
| Composite
resistance of resistors connected in parallel |
Resistance
R1, R2 and R3.

|
| 3--phase
AC circuit |
| When balanced 3-phase AC with line
voltage E (V) is applied to a delta
(¥Ä) or star (Y) connected load, relationships
among voltage, current and electric
power are as follows. |
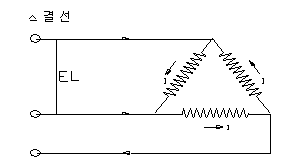 |
IL = ¡î3I (A)
I = EL / R (A)
W = 3ELI = ¡î3IELIL (W) |
|
 |
EL = ¡î3I E (V)
I = IL = E / R = EL / ¡î3R (A)
W = 3EI = ¡î3ELIL (W)
EL = line voltage (V)
IL = line current (A)
I = phase current (A)
R = resistance (¥Ø)
W = electric power (W)
E = line-to-neutral voltage (V) |
|
|
| Ohm¡¯s
law diagram |
..........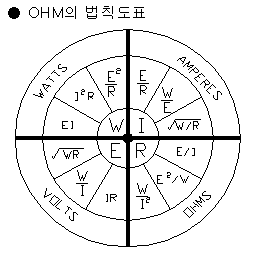 |
| Calculation
of kw in an electric heater |
(A) kw =
weight (kg) ¡¿ specific heat ¡¿ temperature
rise (¡ÆC) / 860
(B) kw = w/§² (by the heat loss table) ¡¿ surface
area (§²) / 1000 |
| In
case of a liquid heater |
(1) kw necessary
to raise the temperature of the liquid to
the desired level in an hour:
......kw = A
+ B / 2
(2) In case of continuous work:
......kw = A
(including the liquid increased) + B |
| Calculation
of power consumption by a fan heater |
Formula:
m3/min ¡¿ 60 min ¡¿ 1.3 (specific weight of
air in kg) ¡¿ 0.242 (specific heat of air)
¡¿ ( ) ¡ÆC temperature = §»
§» ¡À 860 §º ¡¿ 1.2 (electrical efficiency 80%)
= §Ò
Units: m3/min = Amount of wind per minute
.........
Specific weight of air )kg)= 1.3
.........
Specific heat of air = 0.242
.........
1§Ò/hr = 860§»
¡Ø However, it depends on the direction of
air flow, whether direct or curved.
Example)) Desired temperature 50oC and
the amount of wind per minute 0. m3/min
..........¢Ñ
0.8¡¿60¡¿1.3¡¿0.242¡¿50¡É = 7,550 §»
..............7,550¡À860=8,779
..............8,779¡¿1.2=10,535
§Ò (10535W) capacity of the heater |
| Calculation
of power consumption in case of heating up
water |
Formula:
Quantity of water ¡¿ temperature rise ¡¿ time
(min) ¡À 1000 (§º) = §»
§»¡À860¡¿1.2 (electrical efficiency) = §Ò
¡Ø However, it depends on the type of the
cap, i.e., open or close.
Example)) Quantity of water 50§¦, temperature
rise 50oC, and time 20 sec (60 minutes;
3 times per minute; 3 times/min ¡¿ 60 = 180
times)
.........¢Ñ
50§¦ ¡¿ 50 ¡¿ 180 = 450,000 §º
.............450,000
¡À 1,000 = 450 §»
.............450
¡À 860 = 0.532 §Ò
.............0.532
¡¿ 1.2 = 0.627 §Ò (627W) |